برای دیدن محتوای سایت روی دکمه دسته بندی کلیک بفرمایید
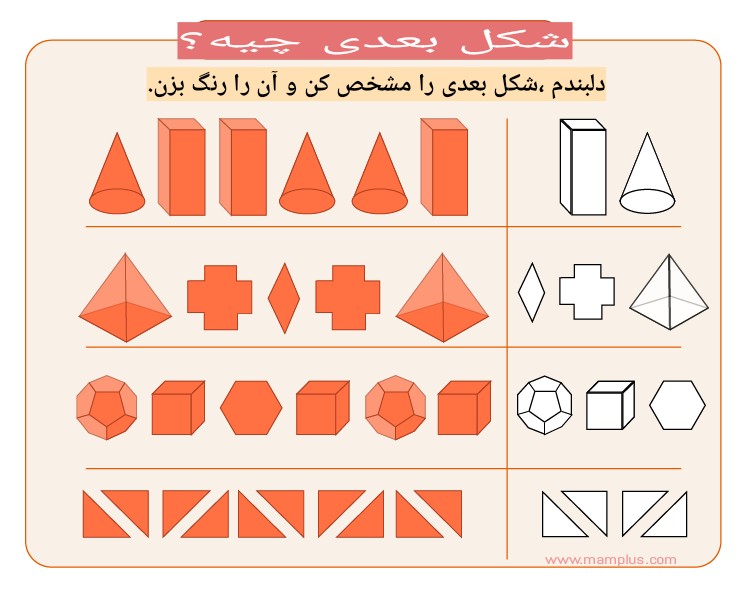
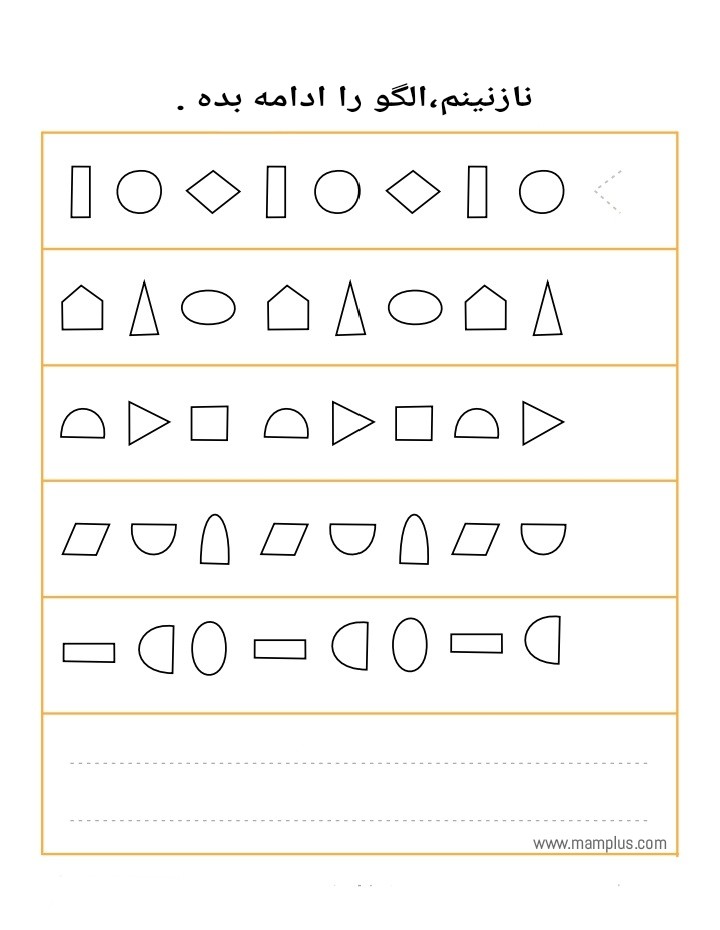
در این تمرین از کودک خواسته میشود که الگوی مشابه الگوی داده شده را بین گزینه ها بیابد : درک الگو به توانایی تشخیص ساختار زیربنایی یک دنباله اشاره دارد. تحقیقات نشان داده است که مهارتهای الگوبرداری و درک الگوی کودکان برای پیشبینی شایستگی ریاضی فعلی و بعدی آنها در اعداد، جبر، و هندسه، و همچنین توانایی خواندن و مهارتهای عملکرد اجرایی است. ریاضیات مبتنی بر الگو و ساختار است، به همین دلیل است که درک الگو برای موفقیت ریاضی بسیار مهم است. الگوسازی به توانایی تشخیص قواعد قابل پیشبینی در اشکال، اعداد و اندازهها، تشخیص همسانی و تفاوت، و ایجاد تمایز، طبقهبندی و برچسبگذاری نیاز دارد. این به کودکان کمک می کند تا بر روی طیف وسیعی از ساختارها و روابط ریاضی تمرکز کنند و بعداً آنها را درک کنند. درک الگوی کودکان در 5 سالگی توانایی ریاضی آنها را در 11 سالگی پیش بینی می کند. در یک مطالعه، مداخلات مبتنی بر آموزش درک الگو در بهبود پیشرفت ریاضی کودکان مؤثرتر از مداخلات مبتنی بر یادگیری ریاضیات عمومی بود . به طور خاص، درک الگوهای تکراری به طور منحصر به فردی با پیشرفت ریاضیات بالاتر مرتبط استو. تصور میشود که توانایی کودکان در انتزاع و شناسایی واحد تکرار در یک الگوی مکرر منجر به پیشرفت ریاضی بالاتری هم در الگوسازی و هم در سایر زمینههای ریاضی میشود. الگوهای تکراری اغلب در ساختارهای ریاضی مانند اندازهگیری (تکرار واحدهای فضایی یکسان) و ضرب (تکرار مقادیر یا اعداد یکسان) رخ میدهند. درک الگو می تواند توانایی های شمارش کودکان را افزایش دهد، زیرا شمارش خود یک توالی قابل پیش بینی و قانونمند است. بچههایی که درک الگوی قوی دارند بعداً در مدرسه در یادگیری الگوها در دنبالههای عددی کمک میکنند، مانند روشی که در هنگام پنجشمارش، رقم واحد بین 0 و 5 تغییر میکند (5، 10، 15، 20، 25، 30، 35…). درک ساختارهای ضربی (ضرب، نسبت، نسبت، مثلثات) شامل درک ایده هایی مانند گروه بندی، تقسیم بندی، یکپارچه سازی و تکرار، و همچنین توانایی در تجسم ساختارهای ریاضی مانند آرایه ها (ماتریسی از ردیف ها و ستون ها) است. مهارت های تجسم ارتباط مثبتی با پیشرفت ریاضی دارد.
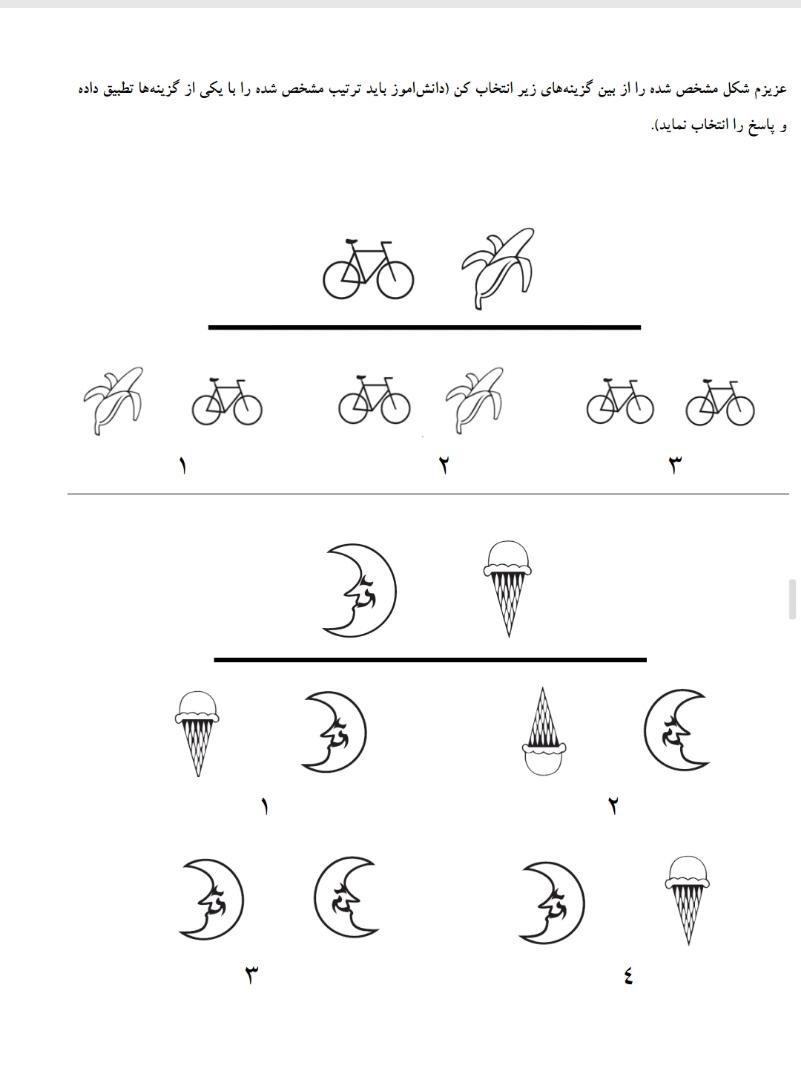
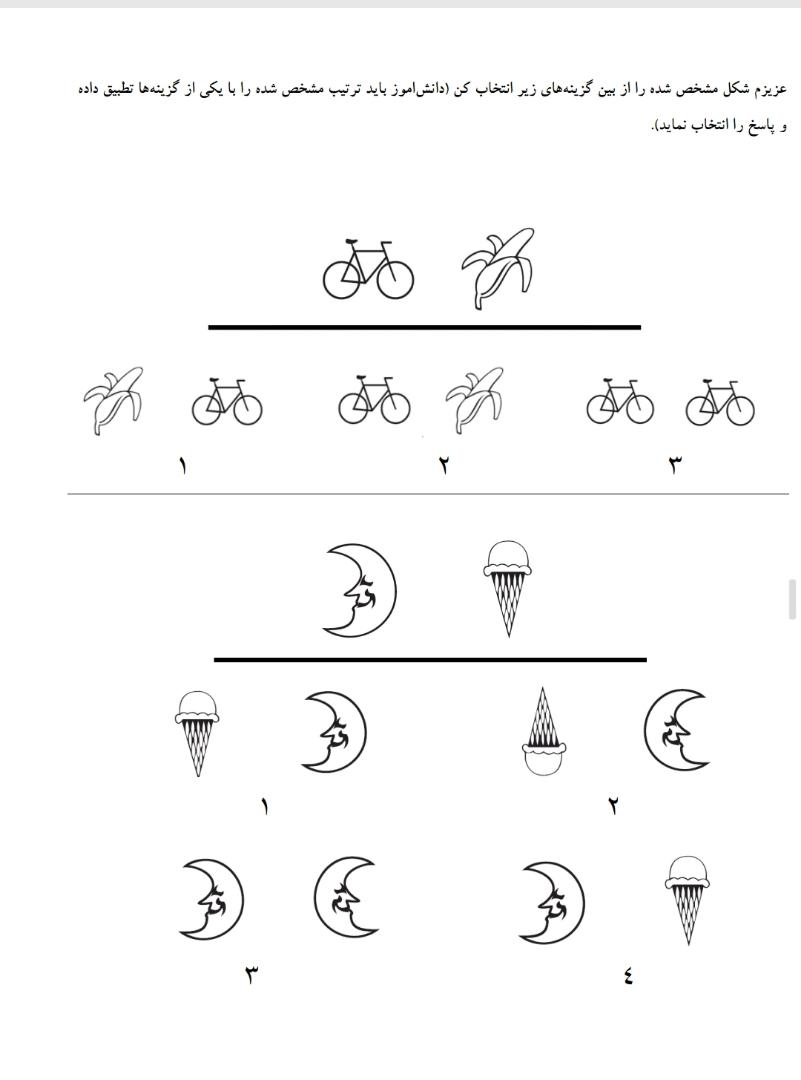
هدف تمرین : اهمیت توالی و ترتیب
بهبود : مهارت های دیداری _ مهارت های تجسمی پیش نیاز مفاهیم ریاضی
هدف های ثانویه : مفاهیم اجتماعی مانند رعایت نوبت
اهمیت درک الگو در دوران کودکی
درک الگو و موفقیت ریاضی: